Logarléc-gyorstalpaló 1. rész

---

Bevezető

Megszoktuk azt, ha bepötyögjük szinte bármilyen kütyübe, hogy „6,3×4”, azonnal kiadja a választ, 24,9-et. Ugyanígy könnyedén tudunk osztani, hatványozni, egyenleteket megoldani, szóval szinte bármilyen műveletet elvégezni olyan eszközökkel, amik "mellesleg" számolni is tudnak. Tud számolni — ez a fenti példában azt jelenti, hogy tud szorozni. Valójában azonban a mikroprocesszorok sem szoroznak, inkább csak összeadnak, és összeadásból építik fel az összes lehetséges műveletet, még az integrálszámítást is. Így tud a gép szorozni. És a kedves Olvasó tud szorozni? Ha a fenti példánál felkapta a fejét az eredmény láttán, akkor tud. Ugyanis az eredmény hibás volt. Sokan annak idején azt hitték, a logarléc-kezelésnél lévő "muszáj" az utánaszámolásra megszűnt az elektronikus számológépek elterjedésével. Valójában ez csak elkényelmesítette az embert, mégpedig annyira, hogy a pékségnél 69 forintos sajtos stangliból ha hatot kérek, úgy mondják ki a 175 forintot, hogy szemükben parányi szikrája sincs a kételkedésnek.

Összeadás

Kezdjük a legelején, adjunk össze. Ha fogunk két vonalzót, és cm-es osztásukkal egymás felé fordítva összetoljuk őket, össze tudunk adni két számot. Az egyik vonalzó 2 cm-es hosszához hozzátoljuk a másik vonalzó 6 cm-es hosszát (a két piros hosszat), és le is olvashatjuk az első vonalzón az összegüket, 8 cm-t. Ezt nevezzük analóg számolásnak, ahol a számoknak (jelen példában) hosszakat feleltetünk meg:

2 cm + 6 cm = 8 cm.

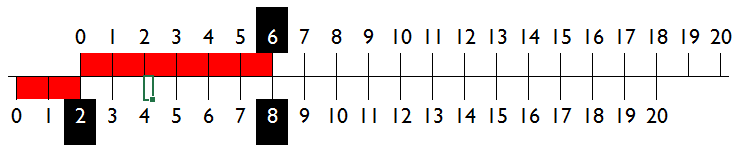
Ki is próbálhatjuk, a felső skálát az egérrel tudjuk mozgatni:

Szorzás

Az előbbi példánál maradva: vajon szerkeszthető-e olyan vonalzó, amin a beosztások segítségével nem összeadni, hanem szorozni lehet? A válasz egészen 1624-ig nem volt egyértelmű: ekkor szerkesztette meg Edmund Gunter az első logaritmikus skálát. Mielőtt bárki megijedne, és akárcsak hosszú képletsorokat vizionálna, lássunk egy igen egyszerű módszert egy ilyen szorzóskála megalkotására. Egy számológép szükségeltetik hozzá, hogy a szorzásokat-osztásokat gyorsabban végrehajthassuk, mintha papíron tennénk.

Logaritmikus skála

Első megközelítésben egy olyan skálát szeretnénk, amivel az 1 és 10 közötti számok szorozhatók. Később meglátjuk majd, hogy ennél többre nincs is szükségünk. Azt szeretnénk tehát, hogy az alsó skálán beállított számhoz (amit szorzunk) tolva a felső skála elejét, a felső skálán lévő adott számnál (amivel szorzunk) megkapjuk az alsó skálán az eredményt, a szorzatot. Tehát, ha most 2-vel szorzunk, akkor az 1-es alatt legyen a 2-es (1×2), a 2-es alatt a 4-es (2×2), a 3-as alatt a 6-os (3×2) és így tovább. Így:

Látható, hogy az alsó sor kétszer olyan gyorsan nő, mint a felső.

Nézzük a 3-mal való szorzást: az 1-eshez a 3, a 2-eshez a 6, a 3-ashoz a 9 tartozik:

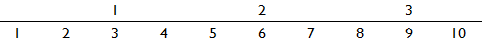
A fentiekből már látható: az 1 és a 2 távolsága pont akkora kell legyen, mint a 2 és a 4, vagy a 3 és a 6 távolsága. Ilyen skálát nem tudunk ilyen egyszerűen szerkeszteni. Keressünk másik utat.

A 2. próbálkozás

Az 1 és a 2 távolságának, ami a 2-vel való szorzásnak felel meg, ugyanakkorának kell lennie, mint a 2 és a 4, vagy a 4 és a 8 távolságának, hiszen ezek mindig kétszeresei az előző számnak. Ezt egyszerűen fel tudjuk rajzolni:

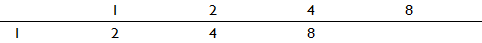
Ebből az tűnik ki, hogy amíg az 1 és a 2 között nincs egész szám, a 2 és a 4 között, ami ugyebár ugyanakkora távolságra van, ott kell lennie a 3-nak, de a 4 és a 8 között már ott kell lennie még három számnak, valahogy így:

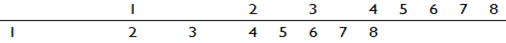
Ez még mindig nem elég pontos, hiszen ha például a 3-as szorzótábláját kívánjuk előállítani, a 3-as alatt a 8-as szám fog szerepelni a 9-es helyett. Finomítani kell tehát a skálánkat.

Utolsó próbálkozás

Most pedig jöjjön a 3. próbálkozás, amit siker fog koronázni. Ugyanilyen elvek szerint fogunk készíteni egy rész-skálát az 1,1-gyel való szorzás alapján. Az 1,1-gyel való szorzások eredményei 1-től kezdve:

1. 1
2. 1,1
3. 1,21
4. 1,331
5. 1,4641
6. 1,61051
7. 1,771561
8. 1,9487171
9. 2,14358881

Ennyi egyelőre elég is. Ezek a számok helyezkednek el tehát egymástól egyenlő távolságokra.

A szakaszok hossza legyen most 1,1 cm, később meglátjuk, ez miért lesz hasznos. Nyilván, mivel a számok közötti távolság folyamatosan csökken, az 1 és az 1,1 között félúton lévő 1,05 érték a felezővonaltól némileg jobbra fog elhelyezkedni. Azonban mivel most egy nagyjából jó skálát szerkesztünk, és nem célunk a nagy pontosság, megelégszünk azzal, hogy ezeket az 1,1 cm-es szakaszokat egyenlő részekre osszuk fel. Mondjuk 8 részre, hogy egyszerű felezésekkel, akár szemmel rajzolva is megszerkeszthessük a részeket. Vegyünk egy A/4-es lapot, és a hosszabbik oldalával párhuzamosan kezdjünk el rajzolni.

Így tehát az első szakasz:

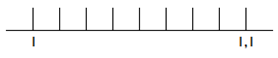
Ha a két szakaszhatár különbségét elosztjuk 8-cal, megkapjuk az egy rész hosszát, ez itt 0,0125. Tehát az első pont 1,0125-öt, a második 1,025-öt, a harmadik 1,0375-öt jelent és így tovább:

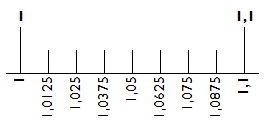
Nézzük a következő szakaszt, ez 1,1-től 1,21-ig tart, így ez 0,11 hosszú, tehát a nyolcadrésze 0,01375, némileg nagyobb, mint az első szakasznál. Ha meg akarjuk találni a 0,2 helyét, akkor célszerű visszafelé kiszámolgatni az egyes osztások értékeit, így ugyebár 1,21 előtti vonás értéke 1,21—0,01375 = 1,19625. Ez kevesebb, mint 1,2, tehát az 1,2 érték a két vonás között helyezkedik el. Rajzoljuk be középre, az utolsó vonás és az 1,21 közé így:

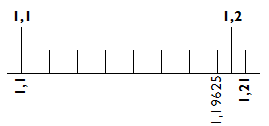
Ugyanezt csináljuk a 3. szakasszal is, ez 1,21-től 1,331-ig tart, egy nyolcadnyi vonás tehát 0,015125. Az utolsó vonás tehát 1,331-0,015125=1,315875. Az utolsó előtti ennél 0,015125-tel kevesebb: 1,30075. Nekünk ez megfelel 1,3-nak, tehát az utolsó előtti vonásra írjuk rá az 1,3-mat:

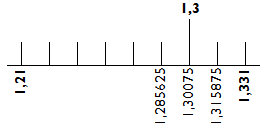
A 4. szakasznál a nyolcadok 0,0166375 hosszúak, tehát az 1,4 visszafelé a 4. vonáshoz tehető:

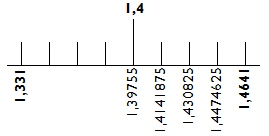
Folytatva a szerkesztést, a 8. szakasszal túljutunk a 2-esen, amit be is tudunk rajzolni az 1,9487171-es szakaszvonal utáni 2. vonásra. Ekkor így néz ki a skálánk:

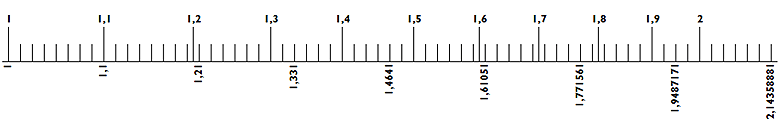
Tovább nem szükséges szerkeszteni, ugyanis a többi egész szám a már felrajzolt távolságokkal előállítható, mégpedig:

2×1,5=3, tehát a 3-as szám ugyanakkora távolságra van a 2-estől, mint az 1-estől az 1,5. Mérjük hozzá a 2-eshez az 1 és az 1,5 távolságát, és jelöljük meg, itt van a 3-as.

A 4-es a legegyszerűbb, az 1-2 távolságot duplázzuk.

Megtehetjük ezt az egészet úgy is, hogy az 1-2 részt átmásoljuk a 2-4 részre, és a számokat megduplázzuk, tehát az 1,1-et az új helyén 2,2-nek, az 1,2-t 2,4-nek stb. írjuk fel.

Az 5-ös 2,5×2. A 2,5 pedig 1,25-ször 2. Az 1,25-öt egyszerűen rajzoljuk be 1,2 és 1,3 közé félúton, és ehhez mérve a 1-2 távolságot, megkapjuk 2,5-öt, majd még egyszer rámérve az 5-ös helyét is.

A 6-ost egyszerűen megkapjuk, ha a 3-ashoz hozzámérjük az 1-2 távolságot.

A 7-es 3,5×2, azaz 1,75×2×2. Az 1,75-öt az 1,7 és az 1,8 közé rajzolva, a fentiekkel azonos módon felrajzoljuk a 7-est.

A 8-as megint egyszerű, a 4-eshez mérjük az 1-2 távolságot.

A 9-es 3×3, a 3-ashoz mérjük az 1-3 távolságot.

A 10-et pedig 5×2-ként tudjuk felvenni. Így tehát megkaptunk egy egyszerű, nem túl pontos logaritmikus skálát 1-től 10-ig:

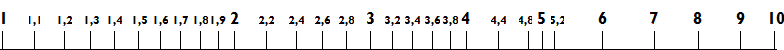
Ha a vonásokat meghosszabbítjuk, majd hosszában kettévágjuk a papírt, máris van két ilyen skálánk, amivel tudunk szorozni, legalábbis a felrajzolt számokkal. Például a 2 × 4 = 8 az alábbi két hossz összegeként adódik:

Itt pedig egy kipróbálható modell, aminek felső skáláját az egérrel tudjuk mozgatni:

És nagyobb számokkal is. Az egyik skálán írjunk minden egész szám után egy nullát, így 10-től 100-ig tartó skálánk lesz. Ezzel is ugyanúgy megy a szorzás. Ugyanezt eljátszhatjuk 100-szor, 1000-szer nagyobb, vagy akár ezerszer kisebb számokkal is.

No és mi a helyzet akkor, ha nem tudjuk leolvasni az eredményt, mert a felső skála annyira kilóg jobbra, hogy a keresett szám nincs rajta az alsó skálán? Elméletben meghosszabbíthatjuk az alsó skálát egy ugyanolyan skálával jobbra, de minden szám tízszeresét ráírva. De észre kell vennünk, hogy ugyanezt kapjuk meg, ha az alsó skálán lévő számhoz (a szorzandóhoz) a felső skála 1-ese helyett a 10-esét állítjuk be.

Az osztás is egyszerűen elvégezhető, itt a szakaszokat kell kivonnunk egymásból: 6:5, azt jelenti, hogy az 1-6 távolságból levonjuk az 1-5 távolságot: az alsó skála 6-osához állítjuk be a felső skála 5-ösét, és a felső skála 1-esénél megkapjuk az eredményt az alsó skálán: 1,2. Ezzel a módszerrel beirogathatjuk vagy csak bevonalkázhatjuk a hiányzó számokat a skáláinkon.

(Milliméterpapírra méricskélés nélkül is felrajzolhatunk egy ilyen skálát, de ott célszerűen 10 részre kell osztanunk az egyes szakaszokat, viszont az eredmény is pontosabb lesz. Ha pedig a szorzótényezőt 1,1 helyett 1,01-nek vesszük, sokkal pontosabb skálát tudunk szerkeszteni.)

Mérjük le utólag, hogy az egyes számok mekkora távolságra vannak az 1-estől. Nyilván függ az alkalmazott szakaszhosszaktól is, ha betartottuk az előírtat, ez 1,1 cm.

Szám	Mért távolság	Kiszámított távolság
1,1	1,1 cm	1,1 cm
1,2	2,1 cm	2,13125 cm
1,3	3 cm	3,025 cm
1,4	3,8 cm	3,78125 cm
1,5	4,6 cm	4,675 cm
1,6	5,4 cm	5,43125 cm
1,7	6,1 cm	6,11875 cm
1,8	6,8 cm	6,80625 cm
1,9	7,4 cm	7,425 cm
2	8 cm	7,975 cm
2,5	10,5 cm	10,55 cm
3	12,6 cm	12,65 cm
3,5	14,4 cm	14,4375 cm
4	16 cm	15,95 cm
5	18,5 cm	18,525 cm
6	20,6 cm	20,625 cm
7	22,4 cm	22,4125 cm
8	23,9 cm	23,925 cm
9	25,3 cm	25,3 cm
10	26,5 cm	26,475 cm

Tulajdonképpen mi is ez a táblázat? Egy egyszerű logaritmustáblázat, az 1-től 10-ig tartó számok logaritmusaival, illetve a logaritmusoknak megfelelő hosszakkal.

Jegyezzük meg a 10-es számhoz tartozó értéket, ez itt 26,5 cm. Mivel a skálánk itt úgymond újrakezdődik (csak az 1,1 helyett 11, az 1,2 helyett 12 lesz, és így tovább), ez lesz az alaphosszunk.

Számoljuk ki számológéppel a valóságos 10-es alapú logaritmusaikat (log gomb), és szorozzuk be az alaphosszal, elég 4 számjegyre pontosan:

Szám (x)	lg x	26,5 × lg x	Szerkesztett távolság
1	0	0	0 cm
1,1	0,04139	1,097	1,1 cm
1,2	0,07918	2,098	2,1 cm
1,3	0,1139	3,02	3 cm
1,4	0,1461	3,872	3,8 cm
1,5	0,1761	4,666	4,6 cm
1,6	0,2041	5,409	5,4 cm
1,7	0,2304	6,107	6,1 cm
1,8	0,2553	6,765	6,8 cm
1,9	0,2788	7,387	7,4 cm
2	0,301	7,977	8 cm
2,5	0,3979	10,55	10,5 cm
3	0,4771	12,64	12,6 cm
3,5	0,5441	14,42	14,4 cm
4	0,6021	15,95	16 cm
5	0,699	18,52	18,5 cm
6	0,778	2062	20,6 cm
7	0,8451	22,4	22,4 cm
8	0,9031	23,93	23,9 cm
9	0,9542	25,29	25,3 cm
10	1	26,5	26,5 cm

Miért is kellett megszorozni 26,5-tel? Mint látjuk, az 1-10 "távolság" 1-re jön ki, tehát ha 1 cm-es skálát szerkesztettünk volna, akkor pontosan a logaritmusok értékeinek megfelelő távolságokban lettek volna az egyes számértékek. (A használt logarléceknél ez az alaptávolság 12,5, 25, vagy 50 cm, illetve angolszász területeken 5, 10 vagy 20 inch.)

Valljuk meg, az egyszerű módszereinkhez képest az elért pontosság nagyon szép eredmény.

A táblázatban az általunk szerkesztett értékek is szerepelnek, összehasonlítás végett.

Kérdezhetnénk, hogy ha ez ilyen egyszerű szerkesztéssel is megoldható, akkor miért nem született meg a logarléc sokkal korábban, miért csak a logaritmus feltalálása/felfedezése után?

Maradhatunk annyiban, hogy — mint láttuk — a logaritmustáblázat megszerkesztése adja az ötletet ezek geometriai ábrázolására, és ez fordítva is igaz.

Egy kis matematika

Talán sikerült egy kicsit megbarátkozni a logaritmussal, így össze is foglalhatjuk a tapasztaltakat:

A skálákat egymás mögé illesztve, látható, hogy mondjuk az 1 és a 2, a 10 és a 20, vagy akár a 0,001 és a 0,002 távolsága ugyanakkora. Ha a skálákat képzeletben egymás mögé rakosgatjuk, akkor az is könnyen belátható, hogy az 1 és 20 távolsága előállítható úgy, hogy vesszük egyrészt az 1 és a 10 távolságát (alaptávolság) és a 10 és a 20 (végsősoron az 1 és a 2) távolságát. Ugyanígy ha mondjuk az 1 és a 3500 távolságát keressük, az előáll:

1. 1 és 10 távolságából
2. 10 és 100 távolságából (azonos az 1 és 10 távolságával)
3. 100 és 1000 távolságából (u.a.)
4. 1000 és 3500 távolságából (ami ugyanannyi, mint az 1 és a 3,5 távolsága)

Írjuk fel úgy, hogy:

3,5 = 0 × alapszakasz + 3,5 távolsága 1-től
35 = 1 × alapszakasz + 3,5 távolsága 1-től
350 = 2× alapszakasz + 3,5 távolsága 1-től
és így tovább.

Az egyszerűség kedvéért vegyük az alapszakaszt most 1-nek. Számoljunk utána géppel (a gépeken az lg helyett az angolszász területeken elterjedt log felirat szerepel):

lg 3,5 = 0,5441
lg 35 = 1,5441
lg 350 = 2,5441

Látjuk, hogy ezek csak a tizedesvessző előtti részükben különböznek egymástól, a törtrészük teljesen azonos. Ez megfelel a fenti észrevételünknek, ahányszor szoroztuk az alapszakaszt, annyi lesz az egészrésze, míg a végén hozzáadott távolság lesz a törtrész.

Az egészrészt a matematikában karakterisztikának, régiesen jellemzéknek, míg a törtrészt mantisszának, régiesen pótléknak nevezzük.

Mi eddig a tizes alapú logaritmusokkal dolgoztunk, amiket Briggs-féle logaritmusnak is neveztek, főleg az 1900-as években. Mit is jelent ez? Nézzük meg a fenti számainkat:

100,5441 = 3,5
101,5441 = 35
102,5441 = 350

Ez az, amit először tanítanak a logaritmusról az iskolában: a hatványozás egyik inverz művelete. Felmerülhet a kérdés, hogy mondjuk szerkeszthető-e ilyen logaritmikus skála 6-os alapú, vagy akármilyen alapú logaritmusok alapján? A válasz igen, de sok értelme nincs.

Egy kis kitérő

log₆ 1 = 0
log₆ 1,712 = 0,3
log₆ 6 = 1
log₆ 10,27 = 1,3
log₆ 36 = 2
log₆ 61,62 = 2,3
log₆ 216 = 3

(Számológéppel nem számolhatunk közvetlenül akármilyen alapú logaritmust, így az alábbi összefüggés szükséges: log₆ x = lg x / lg 6.)

A fentiekben feltűnhet, hogy az 1,712 × 6 = 10,27, illetve 10,27 × 6 = 61,62. A karakterisztikára és a mantisszára való felbontás itt is lehetséges, csak nem olyan látványos. Legalábbis a 10-es számrendszerben nem. Számítsunk át minden értéket 6-os számrendszerbe:

A helyiértékek a következők:

216-osok 36-osok 6-osok 1-esek , (hatodosvessző) 1/6-odok 1/36-odok
63 62 61 60 6-1 6-2

Felírva a fenti táblázat értékeit 6-os számrendszerben:

log₆ 1₆ = 0₆
log₆ 1,413₆ = 0,14₆
log₆ 10₆ = 1₆
log₆ 14,13₆= 1,14₆
log₆ 100₆ = 2₆
log₆ 141,3₆ = 2,14₆

(A tizedesek átváltásakor figyelni kell, mivel a hatodosvessző után 1/6-od részek száma következik, majd az 1/36-od részek száma és így tovább)

Ugyanazt láthatjuk, mint a 10-es alapú logaritmus esetében. Tehát a 6-os alapú logaritmus alapján szerkesztett logarléccel a 6-os számrendszerben tudunk számolni.

Kitérő vége

Nézzük most a szorzást. Hogyan is szoroztunk a skáláinkkal? Egymáshoz illesztettük a két számnak megfelelő hosszakat, magyarul összeadtuk őket. Ez azt jelenti, hogy például:

6,5 × 4 = 1 és 6,5 távolsága + 1 és 4 távolsága.

Ezt felírhatjuk úgy, hogy:

lg (6,5 × 4) = lg 6,5 + lg 4.
lg ab = lg a + lg b.

Itt álljunk meg egy szóra. Ez már némileg láttatja velünk, mire is jó a logaritmus. Ha belegondolunk, hogy papíron kellene szoroznunk mondjuk 8 jegyű számokat egymással, belátható, hogy mennyi rész-szorzást kellene fejben elvégeznünk, ugyebár 8-szor 8-at, azaz 64-et. Mindezek után a rész-szorzatokat még össze is kell adogatnunk helyiértékenként, majd a végén ezeket soronként. Nem egyszerűbb a két szorzandó logaritmusát (melyet kikereshetünk mondjuk logaritmustáblából) összeadni, majd az összeget visszakeresni? Ebben áll a logaritmusok gyakorlati haszna, mégpedig a szorzások, osztások egyszerűbbé tételében. Ma már nyilván ennek nincs jelentősége, de a száraz matematikai képletözönbe egy kis színt lehet vinni vele.

További olvasnivalók

Logarléc-gyorstalpaló 2. rész (hamarosan!)